La Banda de Moebius, uno de los objetos matemáticos más famosos dentro y fuera de la propia matemática
A. F. Möebius hizo el sorprendente descubrimiento de que existen superficies con una sola cara.
La mas simple de estas superficies es la llamada banda de Möebius, formada tomando una larga tira rectangular de papel y uniendo sus extremos después de darle media vuelta a uno de ellos
Un bicho que se arrastrara sobre esta superficie, andando siempre por la parte media de la tira, llegaría a su posición original en el lado inferior, como se aprecia en el dibujo del artista gráfico M. C. Escher (1898-1972)
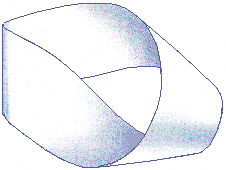
Otra propiedad curiosa de la banda de Möebius es que su contorno está formado por una curva simple cerrada.
Resulta difícil, para cualquiera que no esté familiarizado con la banda de Möebius, predecir este comportamiento, tan contrario a la intuición de lo que "debería" suceder.
Si cortamos la banda de Möebius a lo largo de su línea media se obtiene una línea más larga pero con dos vueltas.
Pero si no la cortamos justo por la mitad se forman dos tiras diferentes, separadas pero entrelazadas.
Pero si no la cortamos justo por la mitad se forman dos tiras diferentes, separadas pero entrelazadas.
Es fascinante jugar con tales tiras, cortándolas de parte a parte a lo largo de líneas paralelas al contorno a distancias de 1/2, 1/3, etc. Prueba a hacerlo.
Algunas utilidades prácticas
Las bandas de Moebius tienen también utilidades prácticas:
1) Películas de cine, en la que se pueden grabar imágenes en ambas caras.
2) La misma idea ha sido aplicada a cintas magnetófonicas, con lo que la cinta retorcida puede funcionar el doble de tiempo que lo que estaría otra normal.
3) Cintas transportadoras diseñadas a fin de que sufran igual desgaste por ambos lados.
4) Filtro autolimpiable destinado a maquinas de limpieza en seco, que por tener la forma de banda de Moebius facilita el lavado por ambas caras de la suciedad depositada en el filtro al ir éste dando vueltas...



